کلاس خصوصی هندسه هفتم تیزهوشان – اثبات برابری زاویه های دو مثلث

کلاس خصوصی هندسه هفتم تیزهوشان – اثبات برابری زاویه های دو مثلث

 

سوال هندسه هفتم مدرسه علوی تهران

در شکل هندسی زیر اگر A و H و K زوایای قائم باشند، اثبات کنید که:

الف) C = M₁

ب) B = E₁

 

 

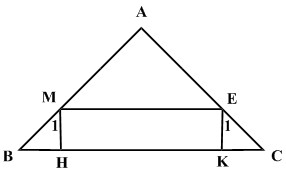
پاسخ:

۱- از مجموع زوایای داخلی مثلث بزرگ داریم:

A + B + C = 180

A = 90

⇓

B + C = 90

۲- از مجموع زوایای داخلی مثلث کوچک سمت چپ داریم:

M₁ + B + H = 180

H = 90

⇓

B + M₁ = 90

۳- از مجموع زوایای داخلی مثلث کوچک سمت راست داریم:

E₁ + K + C = 180

K = 90

⇓

K + E₁ = 90

از برابری معادلات شماره ۱ و ۲ داریم:

 B + C = 90

M₁ + B = 90

⇓

B + M₁ = B + C

⇓

M₁ = C

از برابری معادلات شماره ۱ و ۳ داریم:

 B + C = 90

E₁ + C = 90

⇓

C + E₁ = B + C

⇓

E₁ = B

 

دانش آموزان عزیزم همان طوری که دیدید روش معادله نویسی بهترین راه برای حل این نوع از سوالات اثباتی هندسه می باشد.

 

 

 

تدریس خصوصی و گروهی هندسه هفتم و هشتم و نهم در تهران