آموزش و تدریس هندسه – اثبات مثلث متساوی الساقین درون مستطیل
سوال اثباتی هندسه هفتم
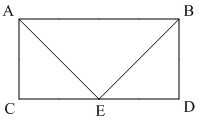
در مستطیل ABCD، نقطه E در وسط CD قرار دارد. اثبات کنید که ABE مثلث متساوی الساقین است.
پاسخ و حل مسئله:
دانش آموزان عزیزم وقتی سوال میگه که اثبات کنید مثلث ABE متساوی الساقین است، در حقیقت میگه که اثبات کنید دو ضلع AE و BE با هم برابرند. چون وقتی این دو ضلع با هم برابر باشند یعنی مثلث ABE متساوی الساقین است.
حال چون این دو ضلع مربوط به دو مثلث جداگانه ACE و BDE می شود بنابراین برای اثبات برابری این دو ضلع کافی است که اثبات کنیم این دو مثلث هم نهشت هستند. چون در این صورت، اجزای نظیر به نظیر دو مثلث هم برابر خواهند شد.
پس داریم:
C = D
AC = BD
CE = DE
⇓
ACE ≅ BDE
⇓
AE = BE
پس بنابراین اثبات کردیم که مثلث ABE متساوی الساقین است.

معلم خصوصی ریاضی و هندسه هفتم و هشتم و نهم در تهران
 Iranian Chemist شیمیدان ایرانی
Iranian Chemist شیمیدان ایرانی