آموزش هندسه به زبان ساده – تدریس اثبات مثلث متساوی الساقین درون مربع

آموزش هندسه به زبان ساده – تدریس اثبات مثلث متساوی الساقین درون مربع

 

سوال هندسه هفتم

در شکل زیر اگر ABCD یک مربع باشد و دو زاویه E₁ و F₁ با هم برابر و مساوی ۴۵ درجه باشند، اثبات کنید که AEF یک مثلث متساوی الساقین است.

 

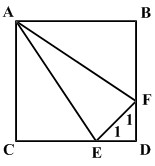
پاسخ:

 

E1 = F1

⇓

مثلث EFD متساوی الساقین است

⇓

ED = FD

حالا از برابری اضلاع مربع خواهیم داشت:

BD = CD

ED = FD

⇓

EC = FB

حالا با برابری دو ضلع و یک زاویه بین آن ها (ض ز ض) از دو مثلث خواهیم داشت:

EC = FB

B = C

AB = AC

⇓

ACE ≅ ABF

حالا که اثبات کردیم این دو مثلث هم نهشت هستند، پس اجزای نظیر به نظیرشان نیز برابر است:

AE = AF

⇓

مثلث AEF متساوی الساقین است

 

 

 

تدریس خصوصی و گروهی هندسه هفتم و هشتم و نهم در تهران