معلم خصوصی هندسه هفتم دانش آموزان بهترین مدارس متوسطه دوره اول تهران

اثبات نصف وتر بودن ضلع روبروی زاویه ۳۰ درجه در مثلث قائم الزاویه

 

سوال هندسه هفتم مدرسه روزبه تهران

اثبات کنید که در هر مثلث قائم الزاویه ضلع روبروی زاویه ۳۰ درجه برابر نصف وتر آن مثلث است.

 

پاسخ:

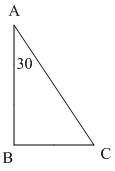
دانش آموزان عزیز برای حل این سوال نسبتا سخت اولین کاری که باید بکنید این است که یک مثلث قائم الزاویه رسم کنید.

 

 

در گام بعدی، دقیقا به اندازه ضلع BC از طرف رأس B رسم کنید و آن را D بنامید. سپس ضلع AD را نیز رسم کنید:

 

 

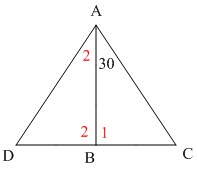
در گام بعدی شروع می کنیم به اثبات هم نهشتی دو مثلث ABC و ABD:

AB = AB

B₁ = B₂

BC = BD

⇓

ABC ≅ ABD

از هم نهشتی این دو مثلث نیز برابری اجزای متناظر را خواهیم داشت:

A₁ = A₂ = 30

B = C = 60

⇓

A = B = C = 60

⇓

مثلث ABC متساوی الاضلاع است.

⇓

AC = DC

حالا از این نتیجه گیری استفاده خواهیم کرد:

AC = DC

DC = 2BC

⇓

AC = 2BC

 

پس بنابراین اثبات کردیم که وتر دو برابر ضلع روبروی زاویه ۳۰ درجه در مثلث قائم الزاویه است.

 

 

 

تدریس خصوصی هندسه و ریاضی هفتم و هشتم و نهم در تهران